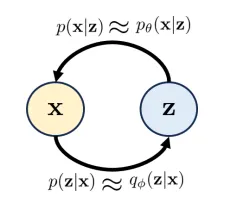
VAE can be considered as an encoder-decoder pair, the structure of which is shown as follows. x \mathbf{x} x z \mathbf{z} z
p ( x ) p(\mathbf{x}) p ( x ) x \mathbf{x} x p ( z ) p(\mathbf{z}) p ( z ) p ( z ) ∼ N ( 0 , I ) p(\mathbf{z})\sim \mathcal{N}(0, \mathbf{I}) p ( z ) ∼ N ( 0 , I ) p ( z ∣ x ) p(\mathbf{z}|\mathbf{x}) p ( z ∣ x ) encoder .p ( x ∣ z ) p(\mathbf{x}|\mathbf{z}) p ( x ∣ z ) decoder .In practice, people often use the following two proxy distributions:
q ϕ ( z ∣ x ) q_{\phi}(\mathbf{z}|\mathbf{x}) q ϕ ( z ∣ x ) p ( z ∣ x ) p(\mathbf{z}|\mathbf{x}) p ( z ∣ x ) p θ ( x ∣ z ) p_{\theta}(\mathbf{x}|\mathbf{z}) p θ ( x ∣ z ) p ( x ∣ z ) p(\mathbf{x}|\mathbf{z}) p ( x ∣ z ) p θ ( x ∣ z ) p_{\theta}(\mathbf{x}|\mathbf{z}) p θ ( x ∣ z ) z \mathbf{z} z x \mathbf{x} x Evidence Lower Bound (ELBO)# ELBO ( x ) = def E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] \text{ELBO}(\mathbf{x}) \overset{\text{def}}{=} \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{p(\mathbf{x},\mathbf{z})}{q_{\phi}(\mathbf{z}|\mathbf{x})} \right] ELBO ( x ) = def E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ] ELBO is a lower bound for the prior distribution log p ( x ) \log p(\mathbf{x}) log p ( x )
log p ( x ) = E q ϕ ( z ∣ x ) [ log p ( x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) p ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) p ( z ∣ x ) × q ϕ ( z ∣ x ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] + E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( z ∣ x ) ] = ELBO ( x ) + D KL ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) ≥ ELBO ( x ) \begin{align} \log p(x) &= \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}[\log p(x)] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{p(x,z)}{p(\mathbf{z}|\mathbf{x})} \right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{p(x,z)}{p(\mathbf{z}|\mathbf{x})} \times \frac{{q_{\phi}(\mathbf{z}|\mathbf{x})}}{q_{\phi}(\mathbf{z}|\mathbf{x})} \right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{p(\mathbf{x},\mathbf{z})}{q_{\phi}(\mathbf{z}|\mathbf{x})} \right] + \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{q_{\phi}(\mathbf{z}|\mathbf{x})}{p(\mathbf{z}|\mathbf{x})} \right] \\ &=\text{ELBO}(x) + \mathbb{D}_{\text{KL}}(q_{\phi}(\mathbf{z}|\mathbf{x})||p(\mathbf{z}|\mathbf{x})) \\ &\geq \text{ELBO}(x) \end{align} log p ( x ) = E q ϕ ( z ∣ x ) [ log p ( x )] = E q ϕ ( z ∣ x ) [ log p ( z ∣ x ) p ( x , z ) ] = E q ϕ ( z ∣ x ) [ log p ( z ∣ x ) p ( x , z ) × q ϕ ( z ∣ x ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ] + E q ϕ ( z ∣ x ) [ log p ( z ∣ x ) q ϕ ( z ∣ x ) ] = ELBO ( x ) + D KL ( q ϕ ( z ∣ x ) ∣∣ p ( z ∣ x )) ≥ ELBO ( x ) To make it more useful in practice, we use some tricks
ELBO ( x ) = def E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x ∣ z ) p ( z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x ∣ z ) ] + E q ϕ ( z ∣ x ) [ log p ( z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − D KL ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) \begin{align} \text{ELBO}(\mathbf{x}) &\overset{\text{def}}{=}\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{p(\mathbf{x},\mathbf{z})}{q_{\phi}(\mathbf{z}|\mathbf{x})} \right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{{p(\mathbf{x|z}) p(\mathbf{z})}}{q_{\phi}(\mathbf{z|x})} \right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}[\log p(\mathbf{x|z})]+\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}\left[ \log \frac{p(\mathbf{z})}{q_{\phi}(\mathbf{z|x})} \right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})}[\log p_{\theta}(\mathbf{x|z})]-\mathbb{D}_{\text{KL}}(q_{\phi}(\mathbf{z}|\mathbf{x})||p(\mathbf{z})) \end{align} ELBO ( x ) = def E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ] = E q ϕ ( z ∣ x ) [ log q ϕ ( z∣x ) p ( x∣z ) p ( z ) ] = E q ϕ ( z ∣ x ) [ log p ( x∣z )] + E q ϕ ( z ∣ x ) [ log q ϕ ( z∣x ) p ( z ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x∣z )] − D KL ( q ϕ ( z ∣ x ) ∣∣ p ( z )) Training VAE and Loss Function# Let’s look at the decoder .
x ^ = decode θ ( z ) \hat{\mathbf{x}}=\text{decode}_{\theta}(\mathbf{z}) x ^ = decode θ ( z ) we make one more assumption that the error between the decoded image x ^ \hat{\mathbf{x}} x ^ x \mathbf{x} x ( x ^ − x ) ∼ N ( 0 , σ dec 2 ) (\hat{\mathbf{x}}-\mathbf{x}) \sim \mathcal{N}(0, \sigma^{2}_{\text{dec}}) ( x ^ − x ) ∼ N ( 0 , σ dec 2 ) σ dec 2 \sigma^{2}_{\text{dec}} σ dec 2 p θ ( x ∣ z ) p_{\theta}(\mathbf{x}|\mathbf{z}) p θ ( x ∣ z )
log p θ ( x ∣ z ) = log N ( x ∣ d e c o d e θ ( z ) , σ d e c 2 I ) = log 1 ( 2 π σ d e c 2 ) D exp { − ∥ x − d e c o d e θ ( z ) ∥ 2 2 σ d e c 2 } = − ∥ x − d e c o d e θ ( z ) ∥ 2 2 σ d e c 2 − log ( 2 π σ d e c 2 ) D ⏟ you can ignore this term \begin{aligned}\log p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})&=\log\mathcal{N}(\mathbf{x}\mid\mathrm{decode}_{\boldsymbol{\theta}}(\mathbf{z}),\sigma_{\mathrm{dec}}^{2}\mathbf{I})\\&=\log\frac{1}{\sqrt{(2\pi\sigma_{\mathrm{dec}}^{2})^{D}}}\exp\left\{-\frac{\|\mathbf{x}-\mathrm{decode}_{\boldsymbol{\theta}}(\mathbf{z})\|^{2}}{2\sigma_{\mathrm{dec}}^{2}}\right\}\\&=-\frac{\|\mathbf{x}-\mathrm{decode}_{\boldsymbol{\theta}}(\mathbf{z})\|^{2}}{2\sigma_{\mathrm{dec}}^{2}}-\underbrace{\log\sqrt{(2\pi\sigma_{\mathrm{dec}}^{2})^{D}}}_{\text{you can ignore this term}}\end{aligned} log p θ ( x ∣ z ) = log N ( x ∣ decode θ ( z ) , σ dec 2 I ) = log ( 2 π σ dec 2 ) D 1 exp { − 2 σ dec 2 ∥ x − decode θ ( z ) ∥ 2 } = − 2 σ dec 2 ∥ x − decode θ ( z ) ∥ 2 − you can ignore this term log ( 2 π σ dec 2 ) D It is just the l 2 \mathcal{l}_{2} l 2
We approximate the expectation by Monte-Carlo simulation, then the loss function is
Training loss of VAE:
argmax ϕ , θ { 1 L ∑ ℓ = 1 L log p θ ( x ( ℓ ) ∣ z ( ℓ ) ) − D K L ( q ϕ ( z ∣ x ( ℓ ) ) ∥ p ( z ) ) } \operatorname*{argmax}_{\boldsymbol{\phi},\boldsymbol{\theta}}\left\{\frac{1}{L}\sum_{\ell=1}^{L}\log p_{\boldsymbol{\theta}}(\mathbf{x}^{(\ell)}|\mathbf{z}^{(\ell)})-\mathbb{D}_{\mathrm{KL}}(q_{\boldsymbol{\phi}}(\mathbf{z}|\mathbf{x}^{(\ell)})\|p(\mathbf{z}))\right\} ϕ , θ argmax { L 1 ℓ = 1 ∑ L log p θ ( x ( ℓ ) ∣ z ( ℓ ) ) − D KL ( q ϕ ( z ∣ x ( ℓ ) ) ∥ p ( z )) } What’s more, the KL divergence for two d d d N ( μ 0 , Σ 0 ) \mathcal{N}(\boldsymbol{\mu}_{0},\boldsymbol{\Sigma}_{0}) N ( μ 0 , Σ 0 ) N ( μ 1 , Σ 1 ) \mathcal{N}(\boldsymbol{\mu}_{1},\boldsymbol{\Sigma}_{1}) N ( μ 1 , Σ 1 )
D K L ( N ( μ 0 , Σ 0 ) , N ( μ 1 , Σ 1 ) ) = 1 2 ( T r ( Σ 1 − 1 Σ 0 ) − d + ( μ 1 − μ 0 ) T Σ 1 − 1 ( μ 1 − μ 0 ) + log d e t Σ 1 d e t Σ 0 ) \mathbb{D}_{\mathrm{KL}}(\mathcal{N}(\boldsymbol{\mu}_0,\boldsymbol{\Sigma}_0),\mathcal{N}(\boldsymbol{\mu}_1,\boldsymbol{\Sigma}_1))=\frac{1}{2}\left(\mathrm{Tr}(\boldsymbol{\Sigma}_1^{-1}\boldsymbol{\Sigma}_0)-d+(\boldsymbol{\mu}_1-\boldsymbol{\mu}_0)^T\boldsymbol{\Sigma}_1^{-1}(\boldsymbol{\mu}_1-\boldsymbol{\mu}_0)+\log\frac{\mathrm{det}\boldsymbol{\Sigma}_1}{\mathrm{det}\boldsymbol{\Sigma}_0}\right) D KL ( N ( μ 0 , Σ 0 ) , N ( μ 1 , Σ 1 )) = 2 1 ( Tr ( Σ 1 − 1 Σ 0 ) − d + ( μ 1 − μ 0 ) T Σ 1 − 1 ( μ 1 − μ 0 ) + log det Σ 0 det Σ 1 ) In our case, it can be simplified as follows:
D K L ( q ϕ ( z ∣ x ( ℓ ) ) ∥ p ( z ) ) = 1 2 ( ( σ ϕ 2 ( x ( ℓ ) ) ) d + μ ϕ ( x ( ℓ ) ) T μ ϕ ( x ( ℓ ) ) − d log ( σ ϕ 2 ( x ( ℓ ) ) ) ) \mathbb{D}_{\mathrm{KL}}(q_{\boldsymbol{\phi}}(\mathbf{z}|\mathbf{x}^{(\ell)})\parallel p(\mathbf{z}))=\frac{1}{2}\left((\sigma_{\boldsymbol{\phi}}^{2}(\mathbf{x}^{(\ell)}))^{d}+\boldsymbol{\mu}_{\boldsymbol{\phi}}(\mathbf{x}^{(\ell)})^{T}\boldsymbol{\mu}_{\boldsymbol{\phi}}(\mathbf{x}^{(\ell)})-d\log(\sigma_{\boldsymbol{\phi}}^{2}(\mathbf{x}^{(\ell)}))\right) D KL ( q ϕ ( z ∣ x ( ℓ ) ) ∥ p ( z )) = 2 1 ( ( σ ϕ 2 ( x ( ℓ ) ) ) d + μ ϕ ( x ( ℓ ) ) T μ ϕ ( x ( ℓ ) ) − d log ( σ ϕ 2 ( x ( ℓ ) )) ) Reference# [1] Chan, Stanley H. “Tutorial on Diffusion Models for Imaging and Vision.” arXiv preprint arXiv:2403.18103 (2024).
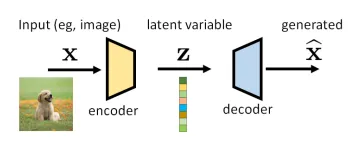 “Variational” comes from the fact that we use probability distribution to describe and . To see more details, we need to consider following distributions:
“Variational” comes from the fact that we use probability distribution to describe and . To see more details, we need to consider following distributions: